Heber Gabriel Pico Jiménez MD,
Medico Cirujano
heberpico@hotmail.com
Calle 13 No.10-40 Cereté, Córdoba, Colombia
Resumen
Se puede fácilmente interpretar resumidamente que este trabajo a partir de la “Ley Universal del efecto Doppler” demuestra precisamente es a la prueba experimental más contundente quizá que tiene a su favor la relatividad general como teoría, tal como es el experimento de Pound Rebka, se manifiesta aquí que esa prueba resulta ser justamente un Doppler transversal doble especialmente descrito por una onda gravitatoria.
Palabras claves: Efecto Doppler, Doppler Relativista, Doppler Sonoro, Dilatación del Tiempo, Corrimiento al Rojo gravitacional.
Abstract
You can easily interpret briefly showing the work of the "universal of the Doppler law" precisely is stronger experimental proof perhaps that has in its favour the gtr as theory, such as the Pound Rebka experiment manifests here that this test is to be just a transverse dual Doppler especially described by a gravitational wave.
Key Words: Doppler Effect, relativistic Doppler, Doppler Caustic, time dilation, landslide the gravitational red.
1. INTRODUCCIÓN
En esta introducción vamos a hacer o dejar un pequeño bosquejo del trabajo anterior de la Ley universal del efecto Doppler trabajado con observador en reposo con respecto a la fuente.
EFECTO DOPPLER RELATIVISTA
En el Doppler relativista “La relación entre las frecuencias al cuadrado más el cuadrado de la relación entre las velocidades, es igual a la unidad”, la siguiente relación mide el grado de corrimiento hacia el azul:
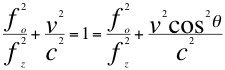 (1)
(1)
Donde fo es la frecuencia emitida por la fuente, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, v es la velocidad de la fuente, c es la velocidad de la luz en el vació y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
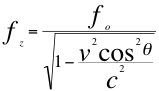 (2)
(2)
Donde fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente, c es la velocidad de la luz en el vació y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
En el Doppler relativista aplicamos nuevamente la ley universal del Doppler de que la “relación entre las frecuencias al cuadrado más el cuadrado de la relación entre las velocidades es igual a la unidad”, la siguiente relación mide el grado de corrimiento hacia al rojo:
 (3)
(3)
Donde f es la frecuencia tal y como la percibe el observador, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, v es la velocidad de la fuente, c es la velocidad de la luz en el vació y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
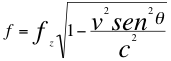 (4)
(4)
Donde f es la frecuencia tal y como la percibe el observador, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, ves la velocidad de la fuente, c es la velocidad de la luz en el vació y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
Entonces el valor de fz de la anterior ecuación número dos (2) la reemplazamos en la también anterior relación número cuatro (4) y nos queda de esa manera, la siguiente y definitiva relación número cinco (5) del efecto Doppler relativista:
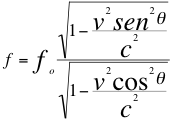 (5)
(5)
θ < 90º
Donde f es la frecuencia tal y como la percibe el observador, fo es la frecuencia emitida por la fuente, ves la velocidad de la fuente, ces la velocidad de la luz en el vacío y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
En esta relación anterior del efecto Doppler relativista cuando, el ángulo θ descrito entre la trayectoria de la fuente y el observador vale cero (0) grados exactamente, la relación queda de la siguiente manera:
 (6)
(6)
θ = 0º
Donde f es la frecuencia tal y como la percibe el observador, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente, ces la velocidad de la luz en el vacío.
En esta misma relación del efecto Doppler relativista cuando, ese ángulo θ tiene un valor que oscila de la siguiente manera entre 0<θ<90, la relación queda de la siguiente manera:
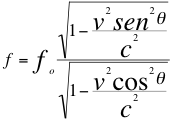 (5)
(5)
θ < 90º
Donde f es la frecuencia tal y como la percibe el observador, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente, ces la velocidad de la luz en el vacío y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
Si el ángulo θ es de un valor de 90 grados exactamente entonces la relación del efecto Doppler relativista, queda la de un Doppler transversal de la siguiente manera:
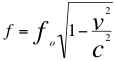 (7)
(7)
θ = 90º
Donde f es la frecuencia tal y como la percibe el observador, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente, ces la velocidad de la luz en el vacío.
Si el ángulo θ toma valores correspondiente entre 90<θ<180 grados entonces la relación del Doppler relativista quedará de la siguiente manera:
 (8)
(8)
θ > 90º
Donde f es la frecuencia tal y como la percibe el observador, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente, ces la velocidad de la luz en el vacío y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
Cuando el ángulo θ es de 180 grados exactamente, entonces la relación del efecto Doppler relativista queda nuevamente de la siguiente manera:
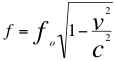 (7)
(7)
θ = 180º
Donde f es la frecuencia tal y como la percibe el observador, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente, ces la velocidad de la luz en el vacío.
EFECTO DOPPLER SONORO.
En el efecto Doppler sonoro la “Ley Universal del Efecto Doppler” dice que “La relación entre las frecuencias emitidas y percibidas mas, la relación entre las velocidades de la fuente y la velocidad del sonido en el aire en reposo es igual a la unidad” es pues una relación lineal.
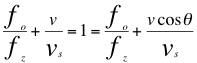 (9)
(9)
Donde fo es la frecuencia emitida por la fuente, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul para ese receptor, ves la velocidad de la fuente, vses la velocidad del sonido y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
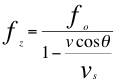 (10)
(10)
Donde fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul para ese receptor, fo es la frecuencia emitida por la fuente, ves la velocidad de la fuente, vs es la velocidad del sonido y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
En el Doppler sonoro aplicamos nuevamente la ley universal del Doppler de que la “relación entre las frecuencias más la relación entre las velocidad de la fuente y la velocidad del sonido es igual a la unidad”, la siguiente relación mide el grado de corrimiento hacia al rojo:
 (11)
(11)
Donde f es la frecuencia percibida por el receptor observador, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, v es la velocidad de la fuente, vs es la velocidad del sonido y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
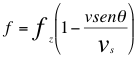 (12)
(12)
Donde f es la frecuencia percibida por el receptor observador, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, v es la velocidad de la fuente, vs es la velocidad del sonido y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
Entonces el valor de fz en la anterior ecuación número diez (10) la reemplazamos en la también anterior relación número doce (12), nos queda entonces de esa forma la siguiente y definitiva relación número trece (13) del efecto Doppler sonoro:
 (13)
(13)
Donde f es la frecuencia percibida por el receptor observador, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente, vs es la velocidad del sonido y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
En esta relación anterior del efecto Doppler sonoro cuando, el ángulo θ descrito entre la trayectoria de la fuente y el observador vale cero (0) grados exactamente, la relación queda de la siguiente manera:
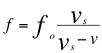 (14)
(14)
θ = 0º
Donde f es la frecuencia percibida por el receptor observador, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente y vs es la velocidad del sonido.
En esta misma relación del efecto Doppler sonoro cuando, ese ángulo θ tiene un valor que oscila de la siguiente manera entre los rangos de 0<θ<90, la relación queda de la siguiente manera:
 (15)
(15)
0º < θ < 90º
Donde f es la frecuencia percibida por el receptor observador, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente, vs es la velocidad del sonido y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
Si el ángulo θ es de un valor de 90 grados exactamente, entonces la relación del efecto Doppler sonoro, queda la de un Doppler transversal de la siguiente manera:
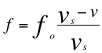 (16)
(16)
θ = 90º
Donde f es la frecuencia percibida por el receptor observador, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente y vs es la velocidad del sonido.
Si el ángulo θ toma valores correspondientes entre el rango de 90<θ<180 grados entonces la relación del Doppler sonoro quedará de la siguiente manera:
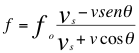 (17)
(17)
90º < θ < 180º
Donde f es la frecuencia percibida por el receptor o, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente, vs es la velocidad del sonido y θ es el ángulo del observador con respecto a la trayectoria de la fuente.
Cuando el ángulo θ es de 180 grados exactamente, entonces la relación del efecto Doppler sonoro queda de la siguiente manera:
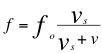 (18)
(18)
θ = 180º
Donde f es la frecuencia percibida por el receptor observador, fo es la frecuencia emitida por la fuente, v es la velocidad de la fuente y vs es la velocidad del sonido.
La última conclusión de este trabajo que fue como una predicción de que puede ser corroborada en la práctica, pensamos que si en realidad nosotros estamos en lo cierto cuando el ángulo θ tenga un valor de 45 grados, la frecuencia f finalmente observada si es una onda electromagnética o, percibida por el receptor si es una onda acústica, será equivalente a la misma frecuencia fo emitida. Esto significa que en realidad el Doppler transversal comienza a correrse hacia el rojo desde que el ángulo que alcanza un valor de 45 grados.
2. DESARROLLO DEL TEMA.
La descripción y el desarrollo de artículo tienen como principio de que si se hace el estudio completo del Doppler, es necesario incluir a la velocidad y trayectoria tanto de la fuente como del observador, que serán descompuestas cada una en dos componentes con respecto al ángulo que describen las trayectorias de cada uno en relación a la recta de vista que los une. Habrán dos vectores que comparten la misma recta de acción y aplicados fijamente en los extremo de dicha recta de visión, estarán situados allí los cosenos de los respectivos ángulos que describen la trayectoria de la fuente y observador vfcosθf y vocosθo con la línea de vista. Vectores que tendrían la misma dirección que podía ser en el mismo sentido o sentido contrario. Por el otro lado estaría el seno del ángulo descrito entre la trayectoria de la fuente y observador vfsenθf y vosenθo que serían siempre paralelas en uno u otro sentido en el mismo plano.
![]() (19)
(19)
![]() (20)
(20)
Donde vf es la velocidad de la fuente, θf es el ángulo descrito entre la línea de visión del observador y la trayectoria de la fuente, vo es la velocidad del observador, θo es el ángulo descrito entre la línea de visión y la trayectoria del observador.
Ahora aplicamos la “Ley universal del efecto Doppler” donde quedan implícitas las velocidades y trayectorias de la fuente y observador: “El cuadrado de la relación entre las frecuencias emitida y observadas más, el cuadrado de la relación entre la velocidad de la fuente y la onda más, el cuadrado de la relación de la velocidad del observador y la onda es igual a la unidad”.
 (21)
(21)
Donde fo es la frecuencia emitida por la fuente, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació.
Vamos a aplicar la ley universal del efecto Doppler a los cosenos de los respectivos ángulos fuente y observador para encontrar o identificar a fz que es la frecuencia emitida de la fuente corrida hacia el azul:
 (22)
(22)
Donde fo es la frecuencia emitida por la fuente, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la línea de visión.
 (23)
(23)
Ahora vamos a aplicar la ley universal del efecto Doppler a los senos de los respectivos ángulos y a calcular a la frecuencia final definitiva que seguramente tendría corrimiento hacia el rojo:
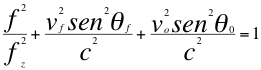 (24)
(24)
Donde f es la frecuencia observada, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
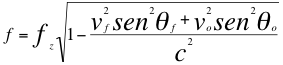 (25)
(25)
Reemplazando a fz de la relación veintitrés (23) en la también anterior relación veinticinco (25) nos queda la siguiente ecuación veintiséis (26):
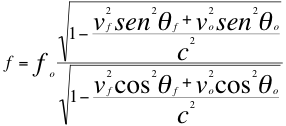 (26)
(26)
θf , θo < 90º
Donde f es la frecuencia observada, fo es la frecuencia emitida por la fuente, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de vista, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
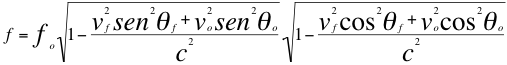 (27)
(27)
θf , θo > 90º
Las anteriores relaciones número veintiséis (26) y veintisiete (27) son las ecuaciones que describen el Doppler relativista cuando la fuente y observador se acercan o se alejan incluso con desiguales velocidades angulares.
Para el Doppler relativista en las ondas electromagnéticas es descrita por las anteriores relaciones pero, para el Doppler sonoro quedaría de la siguiente manera:
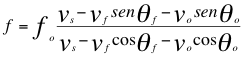 (28)
(28)
Donde f es la frecuencia observada, fo es la frecuencia emitida por la fuente, vs es la velocidad del sonido, vf es la velocidad de la fuente, vo es la velocidad del observador, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
EXPERIMENTO DE POUND Y REBKA
Si un observador a cierta altura de la superficie de la tierra y con cierta velocidad angular ocasionada por la carga rotatoria en reposo, mira una fuente también en reposo con carga rotatoria simétricamente esférica también ubicada en la superficie del planeta. Fuente y observador presentan similares velocidades angulares porque soportan la misma carga rotatoria pero describen diferentes velocidades lineales, velocidades que si la dividimos en sus dos componentes ortogonales con respecto a sus respectivos ángulos descritos en su trayectoria son, la componente vfcosθf para la fuente y vocosθo para el observador, incluso que son nulas porque ellos ni se acercan ni se alejan relativamente entre sí. El Doppler que se describe entonces entre ellos es un Doppler transversal porque el ángulo θf y θo descritos son ambos de 90 grados. Tal como lo plantea el experimento de Pound y Rebka. Entonces la velocidad que llevan la fuente y el observador respectivamente es totalmente la velocidad tangencial originada por la carga rotatoria de cada uno o sea vfsenθf y vosenθo de la siguiente manera a sabiendas de que senθf =1=senθo:
![]() (29)
(29)
Donde vf es la velocidad de la fuente, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión con el observador, r es el radio del planeta, T es el periodo y ω es la velocidad angular de la fuente.
![]() (30)
(30)
Un observador que está hipotéticamente ubicado en reposo a cierta altura h del planeta con igual velocidad angular que la fuente de la superficie, por la carga rotatoria describe también una componente tangencial de la velocidad en el mismo sentido y dirección, entonces se incluye también en la ley universal del efecto Doppler a la velocidad tangencial del observador de la siguiente manera:
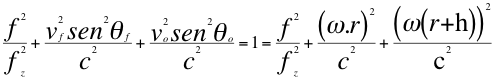 (31)
(31)
Donde fz =fo es la frecuencia emitida por la fuente, f es la frecuencia tal como la mediría un observador situado en reposo a mayor altura, r es el radio del planeta, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión con observador, ω es la velocidad angular de la fuente y observador,hes a la altura sobre la superficie del planeta donde se encuentra el observador, c es la velocidad de la luz.
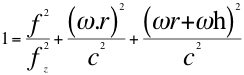 (32)
(32)
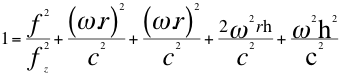 (33)
(33)
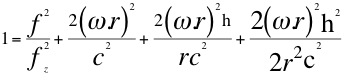 (34)
(34)
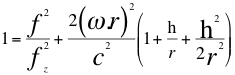 (35)
(35)
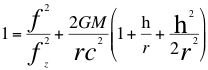 (36)
(36)
Donde fz=fo es la frecuencia emitida por la fuente, f es la frecuencia tal como la mediría un observador a mayor altura, r es el radio del planeta, G es la contante de gravitación universal, M es la masa del planeta, c es la velocidad de la luz,hes a la altura sobre la superficie del planeta donde se encuentra el observador.
Entonces el Doppler transversal o la frecuencia final medida a cierta altura por un observador que tiene velocidad angular idéntica a la de la fuente, frecuencia procedente de una fuente ubicada en reposo en la superficie de un planeta que es la siguiente:
 (37)
(37)
Donde fz=fo es la frecuencia emitida por la fuente, f es la frecuencia tal como la mediría un observador a mayor altura, r es el radio del planeta, G es la contante de gravitación universal, M es la masa del planeta, c es la velocidad de la luz,hes a la altura sobre la superficie del planeta donde se encuentra el observador.
Este siguiente factor que tiene la anterior relación parece coincidir con el originador del múltiplo del Radio de Schwarzschild utilizado para describir a partir de un valor de 3/2 para objetos en órbitas circulares.
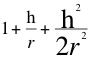 =1,000003527536636886549989067738 (38)
=1,000003527536636886549989067738 (38)
Donde hes a la altura donde se encuentra ubicado el observador medido sobre la superficie del planeta, r es el radio del planeta.
h = 22,5 metros
r = 6.278.400 metros
GRAVEDAD CUANTICA
Si partimos del principio de que la gravedad es una onda que cuenta con una velocidad igual a la de la luz entonces como onda se le puede aplicar, la ley universal del efecto Doppler de la siguiente manera:
 (39)
(39)
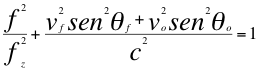 (40)
(40)
Donde fo es la frecuencia emitida por la fuente, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, f es la frecuencia ondulatoria tal y como la mide el observador, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la línea de vista, c es la velocidad de la luz.
De las anteriores relaciones número treinta y nueve (39) y cuarenta (40) obtenemos los dos siguientes factores de dilatación y contracción gravitacional del tiempo tal como lo expresan las siguientes relaciones:
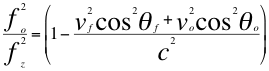 (41)
(41)
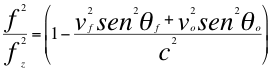 (42)
(42)
Donde fo es la frecuencia ondulatoria emitida por la fuente, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, f es la frecuencia ondulatoria tal y como la mediría un observador, vf es la velocidad de la fuente, vo es la velocidad del observador, θf es el ángulo descrito por la trayectoria de la fuente y la recta de vista, θo es el ángulo descrito por la trayectoria del observador y la recta de vista, c es la velocidad de la luz.
En las anteriores relaciones número cuarenta y nueve (39) y cuarenta (40) le multiplicamos a su segundo miembro por la masa de la partícula o fuente que se observa y nos quedan de la siguiente manera:
 (43)
(43)
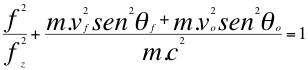 (44)
(44)
Donde fo es la frecuencia ondulatoria emitida por la fuente, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, f es la frecuencia ondulatoria tal y como la mediría un observador, vo es la velocidad del observador, vf es la velocidad de la fuente, θf es el ángulo descrito por la trayectoria de la fuente y la recta de vista, m es la masa invariante de la fuente o partícula observada, θo es el ángulo descrito por la trayectoria del observador y la recta de vista, c es la velocidad de la luz.
Las anteriores relaciones número cuarenta y tres (43) y cuarenta y cuatro (44) quedarían de la siguiente manera:
 (45)
(45)
 (46)
(46)
Donde fo es la frecuencia ondulatoria emitida por la fuente, f es la frecuencia ondulatoria tal y como la mediría un observador, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, θo es el ángulo descrito por la trayectoria del observador y la recta de vista, θf es el ángulo descrito por la trayectoria de la fuente y la recta de vista, m es la masa invariante de la fuente o partícula, c es la velocidad de la luz.
Las anteriores relaciones número cuarenta y cinco (45) y cuarenta y seis (46) son las relaciones de una partícula que se aleja del observador pero, cuando la partícula se acerca al observador se cumplen las siguientes dos relaciones:
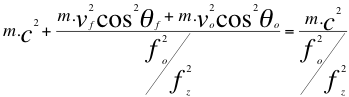 (47)
(47)
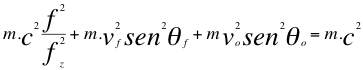 (48)
(48)
Donde fo es la frecuencia ondulatoria emitida por la fuente, f es la frecuencia ondulatoria tal y como la mediría un observador, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, θo es el ángulo descrito por la trayectoria del observador y la recta de vista, θf es el ángulo descrito por la trayectoria de la fuente y la recta de vista, m es la masa invariante de la fuente o partícula, c es la velocidad de la luz.
3. CONCLUSIONES.
a)-La gran conclusión de este trabajo es presentar nada menos que el Doppler relativista general, a partir de la ley universal del efecto Doppler:
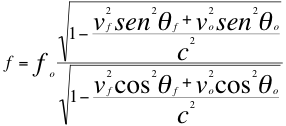 (26)
(26)
θf , θo < 90º
Donde f es la frecuencia observada, fo es la frecuencia emitida por la fuente, vf es la velocidad de la fuente, vo es la velocidad del observador, c es la velocidad de la luz en el vació, θf es el ángulo descrito entre la trayectoria de la fuente y la recta de visión, θo es el ángulo descrito por la trayectoria del observador y la recta de vista.
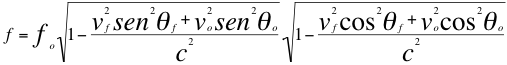 (27)
(27)
θf , θo > 90º
b)-Esta conclusión queremos de nuevo describirla y proponerla como una predicción de este trabajo que puede ser corroborada en la práctica, pensamos que si en realidad nosotros estamos en lo cierto cuando el ángulo θ de una fuente cualquiera observada tenga un valor de 45 grados, la frecuencia f finalmente observada, si es una onda electromagnética o percibida por el receptor si es una onda acústica, será exactamente igual a la misma frecuencia fo emitida. Esto significa que en realidad el Doppler transversal comienza a correrse hacia el rojo desde que el ángulo θ que se describe la fuente tiene un valor de 45 grados.
c)- La gran conclusión de este trabajo es presentar nada menos que la misma solución de Schwarzschild pero deducida a través de la ley universal del efecto Doppler. Presentamos la solución de Schwarzschild pero totalmente resuelta a partir de la descripción de una dilatación transversal del tiempo por velocidad:
 (37)
(37)
Donde fo es la frecuencia ondulatoria emitida por la fuente, f es la frecuencia ondulatoria tal y como la mediría un observador a mayor altura, r es el radio del planeta, G es la contante de gravitación universal, M es la masa del planeta,hes a la altura sobre la superficie del planeta donde se encuentra el observador.
d)-En el movimiento de una partícula como el fotón que se aleja o se acerca a un observador presentamos las siguientes relaciones:
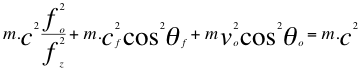 (49)
(49)
 (50)
(50)
Donde fo es la frecuencia ondulatoria emitida por la fuente, f es la frecuencia ondulatoria tal y como la mediría un observador, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, θo es el ángulo descrito por la trayectoria del observador y la recta de vista, θf es el ángulo descrito por la trayectoria de la fuente y la recta de vista y m es la masa invariante de la fuente, fotón o partícula, c es la velocidad de la luz.
 (51)
(51)
 (52)
(52)
Donde fo es la frecuencia ondulatoria emitida por la fuente, f es la frecuencia ondulatoria tal y como la mediría un observador, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, θo es el ángulo descrito por la trayectoria del observador y la recta de vista, θf es el ángulo descrito por la trayectoria de la fuente y la recta de vista y m es la masa invariante de la fuente, partícula o fotón, c es la velocidad de la luz.
El factor dilatador fo2/fz2 para el fotón en la anterior relación número cuarenta y cinco (51):
 (53)
(53)
Donde fo es la frecuencia ondulatoria emitida por la fuente, f es la frecuencia ondulatoria tal y como la mediría un observador, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vf es la velocidad de la fuente, vo es la velocidad del observador, θo es el ángulo descrito por la trayectoria del observador y la recta de vista, θf es el ángulo descrito por la trayectoria de la fuente y la recta de vista y m es la masa invariante de la fuente, partícula o fotón, c es la velocidad de la luz.
Refiriéndonos al anterior factor de dilatación por velocidad del fotón, en el ángulo θf descrito entre la trayectoria de la fuente y la línea de vista con el observador, pues en el fotón como partícula, ella es la fuente y es la onda Doppler a la vez por lo tanto, ese ángulo θf jamás podrá ser de cero (0) grados porque el fotón tarda tiempo en llegar al observador luego, el factor nunca llegará a cero (0). Contribuye también a la explicación de todo esto el hecho de que la masa invariante del fotón es casi (0) cero también. Sin embargo si el fotón choca al observador describiendo un ángulo θf de cero (0) grados con respecto a su propia trayectoria y además encuentra un observador que lo recibe en un ángulo θo de 90 grados, es porque precisamente el fotón se está moviendo en un campo gravitacional de M cumpliendo un Doppler transversal doble y entonces la dilatación del tiempo para el fotón será la siguiente dilatación gravitacional del tiempo.
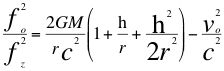 (54)
(54)
Donde fo es la frecuencia ondulatoria emitida por la fuente, fz es la frecuencia emitida por la fuente pero ya corrida hacia el azul, vo es la velocidad del observador, M es la masa que origina al campo gravitatorio, G es la constante de gravitación universal, h es la altura sobre la superficie del cuerpo másico, r es el radio del cuerpo másico, c es la velocidad de la luz.
4. REFERENCIAS DEL PRESENTE ARTÍCULO.
[01] Relatividad General
[02] Relatividad General
[03] corrimiento al rojo gravitacional
[04] efecto Doppler relativista
[05] corrimiento al rojo
[06] corrimiento al rojo gravitacional
[07] efecto doppler relativista
[08] efecto doppler relativista
[1]http://www.monografias.com/trabajos-pdf2/concepto-masa-gravitacional-relatividad-especial/concepto-masa-gravitacional-relatividad-especial.pdf
[2] http://www.textoscientificos.com/fisica/articulos/masa-gravitacional-aparente
[3] Hawking, Stephen; and Ellis, G. F. R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4.
[4] Misner, Thorne and Wheeler, Gravitation, Freeman, (1973), ISBN 0-7167-0344-0.
[5] Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
[6] Steven Weinberg, Gravitation and Cosmology: principles and applications of the general theory of relativity, Wiley (1972), ISBN 0-471-92567-5
[7] Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
[8] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[9] Girbau, J.: “Geometria diferencial i relativitat”, Ed. Universitat Autónoma de Catalunya, 1993. ISBM 84-7929-776-X
[10] Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed. edición, Brooks/Cole. ISBN 0-534-40842-7.
[11] Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed. edición, W. H. Freeman. ISBN 0-7167-0809-4.
[12] Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics, 4th ed. edición, W. H. Freeman. ISBN 0-7167-4345-0.
[13] School of Mathematics and Statistics, University of St Andrews (2000). «Biography of Gaspard-Gustave de Coriolis (1792-1843)».
[14] Oxford Dictionary, Oxford Dictionary 1998.
[15] http://www.monografias.com/trabajos-pdf2/matematicas-energia-cinetica-potencial-movimiento/matematicas-energia-cinetica-potencial-movimiento.pdf
5. REFERENCIAS GENERALES EN LA TEORÍA.
[1] http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_relatividad_general
[2] http://es.wikipedia.org/wiki/Atracci%C3%B3n_gravitatoria
[3] http://es.wikipedia.org/wiki/Gravedad_cu%C3%A1ntica
[4] http://es.wikipedia.org/wiki/Problema_de_los_dos_cuerpos
[5] http://es.wikipedia.org/wiki/Problema_de_los_tres_cuerpos
[6] ©2007 Heber Gabriel Pico Jiménez MD.
[7] ©”Concepción dual del efecto Compton”2007
[8] ©”Concepción dual del efecto fotoeléctrico”2007.
[9] ©”Teoría del Todo”2007.
[10] ©”Unidades duales de la contante de Plack”2007.
[11] ©”Trayectoria dual de la luz”2007.
[12] ©”Compton Inverso”2007.
[13] ©”Quinta dimensión del espacio dual”2007.
[14] ©”Compton Inverso y Reflexión Interna Total”2007
[15] http://personales.ya.com/casanchi/fis/ondacorpusculo01.pdf
[16] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/dualidad-onda-coopusculo
[17] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/unidades-duales-constante-planck
[18] http://www.monografias.com/trabajos48/efecto-compton/efecto-compton.shtml
[19] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-compton
[20] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-fotoelectrico-dual
[21] http://www.textoscientificos.com/fisica/efecto-doppler/transverso-oblicuo-de-broglie
[22] http://www.textoscientificos.com/fisica/efecto-doppler/algebra-efecto-doppler
[23] http://www.textoscientificos.com/fisica/gravedad/cuantica-dual
[24] http://www.textoscientificos.com/fisica/gravedad/leyes-kepler-dual
[25] http://www.textoscientificos.com/fisica/constante-kepler-sub-pe
[26] http://www.monografias.com/trabajos-pdf/gravedad-cuantica-dual/gravedad-cuantica-dual.pdf
[27] http://es.wikipedia.org/wiki/Leyes_de_Kepler
[28] http://www.textoscientificos.com/fisica/kepler-cuantico
[29] http://www.textoscientificos.com/fisica/formulacion-matematica-tercera-ley-kepler
[30] http://www.monografias.com/trabajos-pdf/matematica-tercera-ley-kepler/matematica-tercera-ley-kepler.pdf
[31] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.pdf
[32] http://www.textoscientificos.com/fisica/articulos/estructura-dual-nucleos-atomicos
[33] http://www.textoscientificos.com/fisica/articulos/sabor-color-constante-planck
[34] http://www.monografias.com/trabajos-pdf/estructura-dual-nucleos-atomicos/estructura-dual-nucleos-atomicos.shtml
[35] http://www.monografias.com/trabajos-pdf/sabor-color-constante-planck/sabor-color-constante-planck.shtml
[36] http://www.alt64.org/wiki/index.php/L%C3%A1ser
[37] http://www.textoscientificos.com/fisica/articulos/rayo-laser-dual
[38] http://www.monografias.com/trabajos-pdf/helicidad-foton-laser/helicidad-foton-laser.pdf
[39] http://www.textoscientificos.com/fisica/articulos/helicidad-foton-laser
[40] http://www.monografias.com/trabajos-pdf/longitud-onda-movimiento-tierra-particula/longitud-onda-movimiento-tierra-particula.shtml
[41] http://www.monografias.com/trabajos-pdf/masa-dual-vectorial/masa-dual-vectorial.shtml
[42] http://www.textoscientificos.com/fisica/articulos/masa-dual-vectorial
[43] http://www.textoscientificos.com/fisica/articulos/longitud-onda-asociada-planeta-tierra
Copyright © Derechos Reservados.
Heber Gabriel Pico Jiménez MD. Médico Cirujano 1985 de la Universidad de Cartagena. Investigador independiente de problemas biofísicos médicos de la memoria y el aprendizaje entre ellos la enfermedad de Alzheimer.