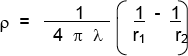Superficies isotermas
Se llaman superficies isotérmicas a las definidas por los puntos del sólido que poseen igual temperatura. La transmisión del calor se dirige en dirección normal a dichas superficies isotermas. Las normales a las superficies coincidirán entonces con las direcciones del flujo calorífico, y se denominan líneas de flujo.
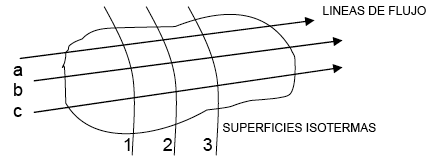
En la figura, se observa un sólido que ha sido cortado con un plano que determina con las superficies isotermas las curvas isotérmicas (1), (2) y (3) de temperaturas t1, t2 y t3.
a, b, c son las líneas de flujo.
Hemos visto que,
![]()
ϕ = - dt Luego: - dt = ϕ dρ
Suponiendo el estado de régimen térmico estacionario, el flujo calorífico permanecerá constante, y siendo dρ la resistencia térmica del material entre las superficies de temperaturas t1 y t2, se obtiene al integrar:
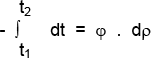
por lo tanto, ϕ ρ = t1 - t2
En consecuencia:
![]()
Problema del muro
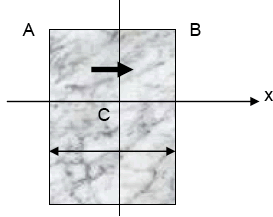
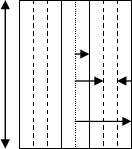
Supongamos un material cuyo coeficiente de conductibilidad es λ se encuentra limitado por dos caras planas y paralelas A y B de superficie S y temperaturas t1 y t2 respectivamente (superficies isotermas).
Si t1 > t2 el calor se transmite de la cara A a la cara B. Las líneas de flujo son normales a ambas caras, es decir paralelas a la dirección del eje x.
Si transcurrido un cierto tiempo se alcanza el estado térmico estacionario o permanente, la temperatura de un punto cualquiera del interior del cuerpo es solamente función de la coordenada x de dicho punto.
Esto significa, que en un plano cualquiera como el C, paralelo a las caras A y B, la temperatura es constante porque t = f(x) para todos los puntos del plano.
Vimos que
![]()
φ = δQ = - λ S dt
Suponiendo que λ es independiente del tiempo y S es constante al integrar entre
x = x1 , x = x2 y t = t1 , t = t2 tendremos:
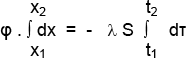
Por lo tanto:
φ (x2 - x1) = λ S (t1 - t 2)
Como x2 - x1 = e, escribimos finalmente:
![]()
En esta forma se calcula el flujo térmico que atraviesa un cuerpo de caras planas y paralelas, conociendo las temperaturas de dichas caras, el valor de la superficie normal al flujo calorífico, el espesor del cuerpo o pared y el coeficiente de conductibilidad del material. En este caso, la resistencia térmica del cuerpo valdrá también:
![]()
Caso de paredes cilíndricas
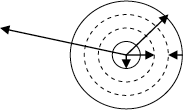
Consideraremos el caso de un cilindro hueco cuyo radio exterior es r2, el interior r1, la conductividad del material λ, t2 la temperatura de la cara exterior, t1 la temperatura de la cara interior y L la longitud del cilindro.
Supongamos que t1 > t2 o sea que el calor fluye de adentro hacia fuera.
Si consideramos un cilindro de espesor muy pequeño dr, y radio r, podemos suponer que las líneas de flujo son prácticamente paralelas dentro del cilindro, aplicando la Ley de Fourier:
![]()
Pues: S = 2 π r. L ; dx = dr
ϕ dr/r = - λ 2 π L dt ;
Integrando, cuando se ha alcanzado el estado térmico estacionario o permanente,
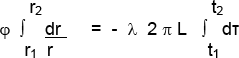
![]()
De donde :
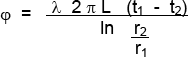
La resistencia térmica valdrá :
![]()
Casos de paredes esféricas
Consideraremos el caso de una esfera sólida hueca de radio interior rr, exterior r2,de la cara interior tt, y exterior t2. Si t1 > t2 el flujo calorífico se dirigirá de adentro hacia fuera. Por las mismas consideraciones del caso anterior:
![]()
pues: S = 4 π r2 ; dx = dr
![]()
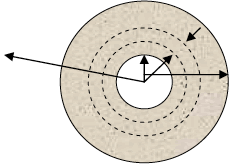
Integrando entre r1 , r2 y t1 , t2 y alcanzando el estado térmico de régimen permanente
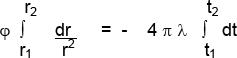
entonces :
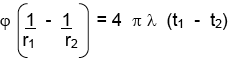
Luego:
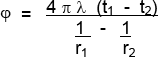
La resistencia térmica será: