Trabajo

Hasta aquí hemos hablado de trabajo sabiendo que es un concepto íntimamente ligado a la energía. Lo que no hemos dicho es cómo expresar matemáticamente el mismo, y aún más: ¿cuántos tipos de trabajo podemos definir? Esta pregunta la contestaremos más adelante, por ahora estudiemos un tipo de trabajo al cual nos referiremos en adelante prácticamente en todos los ejemplos y problemas que se planteen.

Imaginemos un gas (mejor además decir que es un gas ideal) colocado en un cilindro como el de la figura, al cual se lo dilata (expansión del gas):

Gráfico número 3

w = F_ext. (X₂ - X₁)

P_ext. = F_ext. / A

F_ext. = P_ext. ∙ A

Por lo tanto: w = P_ext.∙ A ∙ (X₂-X₁)

A ∙ (X₂ – X₁) = Aumento de volumen durante la expansión o dilatación que es igual a ∆V.

Luego w = P_ext ∙ ∆V

Graficando el proceso con un par de ejes cartesianos en el plano encontramos:

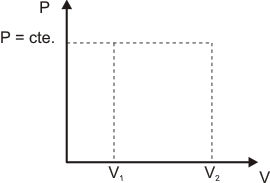
Gráfico número 4

w = P ∙ ∆V = ÁREA

¿Y este mismo proceso puede ser reversible?

Sí, siempre qué: P_ext = P_interna

o mejor: P_ext = P_interna + dP

dP = diferencial de presión o sea un incremento de presión infinitesimal.

Sólo entonces, cuando ello ocurra estaremos en presencia de un proceso reversible termodinámicamente el cual en todo momento debe estar en equilibrio.

¿Eso significa que por haber una diferencia tan pequeña de presión el sistema pude sufrir expansión y/o compresión sin perturbar las condiciones, operando indistintamente en un sentido o en otro?

Precisamente eso constituye el equilibrio, y así se deben realizar los procesos hasta pasar del estado inicial al final.

Es de imaginarse que esto en la vida real es muy difícil de lograr ya que en principio debe realizarse en un tiempo infinito.

Redefinimos ahora la expresión por la que calculamos variaciones de energía interna, tomando como base que el único trabajo que hará el sistema (o que se realiza sobre el) será la expansión (o compresión) de un gas. Recuerde que hemos definido un sistema en el cual sólo tenemos gas lo cual es la condición predeterminada.

Luego:

w = P ∆V

De acuerdo a la convención utilizada en el curso, en un trabajo realizado por el sistema sobre el entorno de expansión, este tendrá signo negativo. Pero ¿del cálculo matemático indicado arriba surge el signo de la convención? : La respuesta es no, ya que presión es una magnitud positiva y ∆V (en una expansión) también lo es, dado lo cual debe cambiarse el signo que nos da la ecuación. Si el caso fuera un trabajo de compresión (realizado por el entorno sobre el sistema), el proceso es a la inversa.

Esta expresión es válida siempre que la contrapresión (P) o presión externa (P_ext) se mantenga constante, porque si no es así, sería distinta.

¿Se podrían plantear sistemas que no fueran gaseosos?

Por supuesto, pero ya nuestros cálculos no serían tan sencillos como cuando usamos gases ideales, y por ello en este texto nos los consideramos.

Trabajo “no-útil” y “útil”

Merece una aclaración el uso de “P”: en nuestro ejemplo y en mucha de la bibliografía, es siempre la presión exterior al sistema, es decir aquella contra la cual se hace el trabajo y como normalmente es la presión atmosférica, por ello se dice que un trabajo de expansión es “trabajo no útil” (ya que se pierde en la atmósfera).

Al trabajo de expansión se lo conceptúa por lo tanto como un trabajo “no útil” pero se debe tener presente que hay casos en los cuales ello no ocurre y por el contrario se lo debe asociar con un trabajo de expansión “útil”. Para diferenciar uno de otro diremos que el trabajo de expansión “no útil” es aquel que se realiza “contra” la presión atmosférica con lo cual la energía intercambiada se considera disipada a la atmósfera, pero el “trabajo de expansión útil” es de acuerdo al siguiente ejemplo:

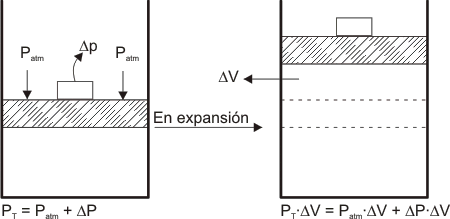
Gráfico número 5

En la figura de arriba la expansión del pistón “contra” la presión atmosférica generará un trabajo de expansión no útil (ya que como dijimos se pierde, no se puede recuperar) pero si al pistón le adicionamos un “sobrepeso” diferente a la presión que ejerce la atmósfera será, de acuerdo a las dos expresiones en las cuales hemos descompuesto el Trabajo:

P_atm ∙ ∆V = Trabajo de expansión contra la P_atm . NO ÚTIL.

∆p ∙ ∆V = Trabajo de expansión contra la Presión “extra” que arbitrariamente hemos colocado: este es un trabajo de EXPANSIÓN ÚTIL ya que la pesa (∆p) queda al final del proceso con una cierta energía potencial mayor al final que al comienzo del proceso.

¿Esto es común en nuestros cálculos? No lo es. Por ello, y en general el trabajo de expansión será no-útil.