Heber Gabriel Pico Jiménez MD.
Médico Cirujano
Calle 13No.10-40 Cereté, Córdoba, Colombia
heberpico@telecom.com.co
Resumen
Este trabajo en resumidas cuentas muestra como, la llamada “Frecuencia de De Broglie” determina al efecto Doppler tanto por la velocidad y dirección relativa de la fuente como, por la velocidad y dirección relativa del observador, en cualquier información partícula u onda que circule entre fuente y observador.
Abstract
This work in short shows like, the call “Frequency of Of Broglie” as much determines to the Doppler effect by the speed and relative address of the source like, by the speed and relative address of the observer, in any information particle or wave that circulates between source and observer.
1. Introducción
Hasta hoy la física teórica acepta por un hecho la longitud de onda de De Broglie a pesar de que se mira con desconfianza por lo pequeña que resulta ser en cuerpos mayores. Esta aparente contradicción es porque se trata de utilizar es la masa total de los cuerpos como si fuera la masa elemental del electrón que transporta el fotón. En las ondas electromagnéticas la masa debe ser la del electrón, porque la que varía en el Doppler es la velocidad.
 (1)
(1)
También está totalmente demostrado matemáticamente en estos trabajos, que el índice de refracción es el inverso del coseno del ángulo de dispersión “teta” del efecto Compton:
![]() (2)
(2)
Nosotros vamos a trabajar no es con la longitud de onda de De Broglie sino precisamente, es con la frecuencia ondulatoria que corresponde exactamente a esa longitud de onda. Es frecuente querer utilizar la masa total de los cuerpos en los cálculos de las ondas electromagnéticas, cuestión que contradice el efecto fotoeléctrico. Pues así resulta una longitud de onda demasiado pequeña equivalente a una exagerada frecuencia afín. Por lo anterior llegamos a la frecuencia que vamos a llamar “Frecuencia de De Broglie” que es la frecuencia emitida por la fuente según la ecuación número tres (3):
![]() (3)
(3)
![]()
Resulta que en este trabajo vamos a manejar esa “Frecuencias de De Broglie” refraccionada por tres tipos de índices de refracción relativos para tres velocidades diferentes. ¿Porqué usamos los índices de refracción si ellos son escrituras de los medios de propagación? Porque precisamente lo que es índice de refracción para un medio de propagación, para las partículas es un “índice de de frecuencias” mejor como un índice de frecuencia en una misma partícula. Son equivalentes. Con el primer índice se nos permite identificar la frecuencia que es recibida por un observador sin haber Doppler, estando fuentes y observador en reposo, ella con su respectiva velocidad e índice de refracción como lo dice la ecuación numero cuatro (4).
![]() (4)
(4)
El segundo índice de fracción sería el que hace la velocidad de la fuente y el ultimo índice, es la “frecuencia de De Broglie” refraccionada por la velocidad del observador, todos descritos respectivamente en las ecuaciones número cuatro (4), cinco (5) y seis (6):
![]()
m = masa del electrón
υD = frecuencia final con Doppler
υ2 = frecuencia final sin Doppler
υf = frecuencia Doppler originada por la velocidad de la fuente
υo = frecuencia de Doppler originada por la velocidad el observador
vf = velocidad de la fuente
vo = velocidad del observador
También vamos a sostenernos sobre la conclusión del trabajo “Concepción dual del efecto Compton”, conclusión que aunque no haya sido aun reconocida por la academia, la presentamos porque consideramos que precisamente este trabajo juega con él un papel de ratificaciones mutuas, ya sea se sirven de pruebas entre ambos trabajos. La conclusión del trabajo “Concepción dual del efecto Compton” es la siguiente:
![]()
En la ecuación número siete (7) se describe solamente el efecto Compton en un solo choque pero, a medida que pasa el tiempo y se sigue desplazando un rayo de luz a través de un medio de propagación cualquiera, siguen ocurriendo más choques sucesivos que no hay formas de contarlos sino a través del tiempo y pasamos a la ecuación número ocho (8).
En la ecuación número ocho (8) tenemos representada la frecuencia final que recibe sin Doppler un observador, partiendo de la frecuencia inicial que surge del emisor, divida entre el primer índice de refracción elevado a la potencia del tiempo más uno (T+1). Nos referimos al tiempo en segundos que tardaría en llegar la onda desde que sale de la fuente hasta alcanzar al observador atravesando un medio de propagación. Prestar atención que el observador está situado a determinada distancia de la fuente, medida por ese tiempo en segundos.
T = tiempo en segundos entre Emisión - Rrecepción
υ2 = frecuencia sin Doppler recibida por el observador
υ1= frecuencia original emitida por la fuente
Para terminar esta introducción, anunciamos que el objetivo de este trabajo es demostrar la responsabilidad que tiene el índice de refracción o “índice de frecuencias” y la “frecuencia de De Broglie” en el efecto Doppler, determinándolo a través de las velocidades y dirección que tienen la fuente y observador.
2. Desarrollo del tema.
El fotón emitido, la fuente y el observador se mueven a diferentes velocidades pero, por ahora vamos a suponer que la fuente y observador se mueven en la misma dirección y sentido del fotón emitido, siendo así se le suman la frecuencia Doppler originada por la velocidad de la fuente, menos la frecuencia Doppler originada por la velocidad del observador como se sugiere en la ecuación numero nueve (9):
![]()

Remplazamos la ecuación número tres (3) y los respectivos índices de refracción para cada uno en la ecuación anterior nos queda de la siguiente manera la ecuación número diez (10):
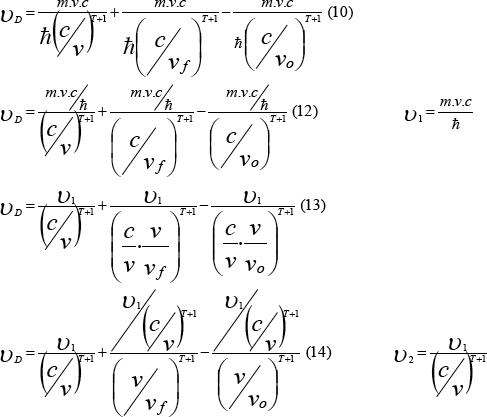
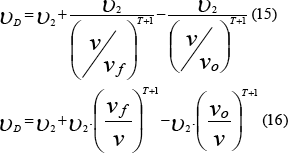
Pero resulta que la fuente y el observador a veces se mueven en direcciones diferentes y necesitamos una expresión matemática que involucre esas posibilidades, entonces debemos incluir el ángulo “alfa” y “beta” que indique la dirección y sentido de la frecuencia. Obtenemos así la ecuación número diez y siete (17):
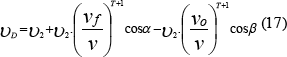
α = ángulo entre dirección de la velocidad de fuente
β = ángulo entre dirección de la velocidad del observador
Todo esto se ilustra en la única figura de este trabajo donde se describen los tres tipos de frecuencias, además los ángulos “alfa” y “beta” construidos. También aclaramos que las direcciones que adoptan las frecuencias Doppler de la fuente y observador, son determinadas por la dirección de sus respectivas velocidades. También vale la pena notar que la emisión de la frecuencia es radial en todas direcciones alrededor de la fuente.

Fig.1 Los puntos rojos de la figura son la masa respectivas de la fuente y el observador
3. Conclusiones.
De la ecuación número diez y siete (17) se pueden desencadenar un sin número de conclusiones pero vamos a seleccionar las más evidentes:
1-El signo y el sentido realmente lo reglamenta el valor y dirección del ángulo “alfa” y “beta” sin necesidad de convenciones nemotécnicas arbitrarias del signo.
2-A simple vista se nota que pueden existir dos tipos de Doppler transversal y oblicuos.
3-Se establece cual es la razón por el cual el ojo humano no puede captar los efectos del Doppler. Precisamente porque se necesitan velocidades elevadas para no quedarse como radiofrecuencia invisibles.
4-Se demuestra lo determinantes que son para los Doppler los índices de refracción.
5-Los índices de refracción son determinantes en la magnitud de las frecuencias Doppler de una onda.
6-Los llamados índices de refracción son las relaciones que existen entre las 2 frecuencias que determinan la frecuencia Doppler.
4. Referencias.
[1] ©2007 Heber Gabriel Pico Jiménez MD.
[2] ©”Concepción dual del efecto Compton”2007.
[3] ©”Concepción dual del efecto fotoeléctrico”2007.
[4] ©”Teoría del Todo”2007.
[5] ©”Unidades duales de la contante de Plack”2007.
[6] ©”Trayectoria dual de la luz”2007.
[7] ©”Compton Inverso”2007.
[8] ©”Quinta dimensión del espacio dual”2007.
[9] ©”Compton Inverso y Reflexión Interna Total”2007
[10] http://personales.ya.com/casanchi/fis/ondacorpusculo01.pdf
[11] http://www.textoscientificos.com/fisica/efecto-fotoelectrico/dualidad-onda-coopusculo
[12]
http://www.textoscientificos.com/fisica/efecto-fotoelectrico/unidades-duales-constante-planck
[13]
http://www.monografias.com/trabajos48/efecto-compton/efecto-compton.shtml
[14]
http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-compton
[15]
http://www.textoscientificos.com/fisica/efecto-fotoelectrico/efecto-fotoelectrico-dual
[16]
http://www.textoscientificos.com/fisica/efecto-fotoelectrico/compton-inverso-reflexion-interna-total
[17] http://www.educaplus.org/luz/refraccion.html
[18] Copyright © Derechos Reservados.