Las moléculas más simples de estudiar, desde el punto de vista de la teoría de orbitales moleculares, son las que están formadas por dos átomos del mismo elemento, esto es, las moléculas diatómicas homonucleares.
Como se ha descrito para la molécula de H2, a partir de dos orbitales atómicos 1s se obtienen dos orbitales moleculares, σg y σu. Los elementos del segundo periodo poseen 4 orbitales de valencia, un orbital s y tres orbitales p, de manera que cuando se combinan 2 átomos de este periodo se pueden obtener un máximo de ocho orbitales moleculares, que adoptan las formas ya mostradas. Los orbitales más internos, los 1s, no se suelen considerar a la hora de construir el Diagrama de Orbitales Moleculares, pues no contribuyen a la formación neta de enlace. Los ocho orbitales moleculares que se forman se pueden clasificar, según la simetría, en dos grupos: cuatro orbitales σ y cuatro orbitales π. Los cuatro orbitales π forman un par doblemente degenerado de enlace y otro par doblemente degenerado de antienlace. El grupo de orbitales σ se distribuye en un amplio rango de energía, siendo uno de ellos un orbital fuertemente enlazante (de muy baja energía) y otro fuertemente antienlazante (de muy alta energía). Los otros dos orbitales σ se sitúan entre estos extremos. Para establecer el diagrama de niveles de energía de estos ocho orbitales moleculares se recurre a métodos como la espectroscopia electrónica de absorción, la espectroscopia de fotoelectrones o a cálculos computacionales. La espectroscopia de fotoelectrones muestra la variación de las energías de los orbitales moleculares para las moléculas diatómicas del segundo periodo, desde el Li2 al F2. Este orden de energía, que es necesario para poder construir la configuración electrónica de la molécula, aparece en la figura para las posibles moléculas diatómicas del segundo periodo. De esta forma puede proponerse un Diagrama de Niveles de Energía para estas moléculas. Es fácilmente observable como hay dos tipos de diagrama, pues el orden relativo de los orbitales 2σg y 1πu es distinto para las moléculas Li2-N2 y para las moléculas de O2 y F2. Como el orden de energía expuesto en la figura es el observado experimentalmente, la explicación debe ajustarse a dicho orden.
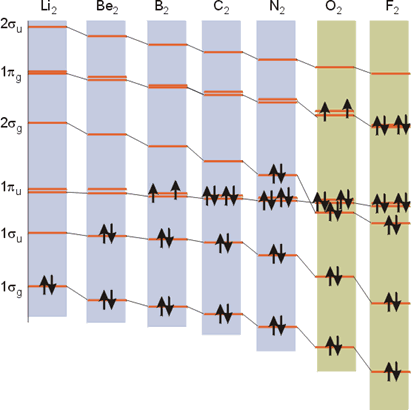
Variación de la energía de los orbitales moleculares de las moléculas Li2-F2. Las capas 1s se consideran propias de cada átomo.
Esta inversión se puede correlacionar con el aumento en la diferencia de energía de los orbitales atómicos 2s y 2p de los átomos que constituyen la molécula, al desplazarse hacia la derecha en el segundo periodo. Recuérdese que para que dos orbitales atómicos puedan mezclarse para dar dos orbitales moleculares, deben presentar simetría y energía similares, algo que no es factible en el caso del O2 y F2, donde la diferencia en energía entre dichos orbitales es mayor.
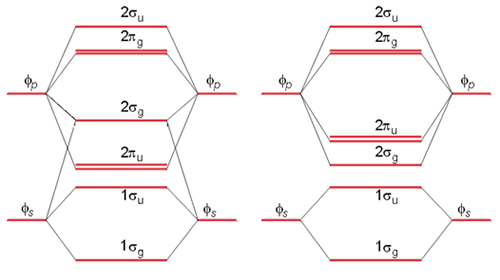
Diagrama de Orbitales Moleculares para las moléculas Li2-N2 (izquierda) y O2-F2 (derecha).
Las configuraciones electrónicas de las moléculas diatómicas homonucleares
Para determinar las configuraciones electrónicas de las moléculas diatómicas homonucleares, y en general, para cualquier molécula, se aplican los mismos principios que para las configuraciones electrónicas de los átomos: el principio de exclusión de Pauli (no más de dos electrones por orbital) y el principio de energía mínima (la ocupación de niveles sigue el orden de energía creciente). Además, si existe más de un orbital con la misma energía (degenerado) disponible para su ocupación los electrones ocuparán estos orbitales separadamente, esto es, con sus espines paralelos, siguiendo la regla de Hund.
Teniendo en cuenta estas reglas, resulta muy simple determinar las configuraciones electrónicas de las moléculas diatómicas homonucleares del primer y segundo periodo.
(a) Moléculas de 1 hasta 4 electrones.
Son las posibles moléculas H2+, H2, He2+ y He2. Sus configuraciones electrónicas son:
H2+: 1σg1 H2: 1σg2 He2+: 1σg2 1σu*1 He2: 1σg2 1σu*2
Aunque en los textos más modernos ya se está eliminando la notación de asterisco para significar el orbital antienlazante, en este curso se va a continuar utilizando, cuando sea posible, dicha notación. Un parámetro de gran importancia es el denominado orden de enlace, que se define de la siguiente forma:
o.e. = ½ (n – n*),
donde n es el número de electrones que ocupan orbitales moleculares enlazantes y n* el número de electrones que ocupan orbitales moleculares antienlazantes.
Según esta definición, los órdenes de enlace para las moléculas de H2+, H2, He2+ y He2 son, respectivamente, 0.5, 1, 0.5 y 0. Como el orden de enlace indica el número de enlaces existentes en la molécula A-A, ello significa que las tres primeras pueden tener existencia real mientras que la última no puede existir. Nótese como la existencia de "medios enlaces", es decir, de órdenes de enlace fraccionarios es una ventaja de la Teoría de los Orbitales Moleculares frente a la Teoría del Enlace de Valencia, que no permite este tipo de consideraciones.
(b) Moléculas de Li2 al N2 .
Teniendo en cuenta el número de electrones de cada elemento así como el orden de energía que aparece en las figuras, se obtienen las siguientes configuraciones electrónicas y órdenes de enlace:
| Li2: KK 1σg2; | o.e. = 1 | enlace simple |
| Be2: KK 1σg2 1σu*2 | o.e. = 0 | |
| B2: KK 1σg2 1σu*2 1πu2 | o.e. = 1 | enlace simple |
| C2: KK 1σg2 1σu*2 1πu4 | o.e. = 2 | enlace doble |
| N2: KK 1σg2 1σu*2 1πu4 2σg2 | o.e. = 3 | enlace triple |
Siendo KK las dos capas 1s de los respectivos átomos.
(c) Moléculas de O2 , F2 y Ne2.
En estos casos hay que tener en cuenta la ya comentada inversión de energía en determinados orbitales moleculares:
| O2 : KK 1σg2 1σu*2 2σg2 1πu4 1πg*2 | o.e. = 2 | enlace doble |
| F2: KK 1σg2 1σu*2 2σg2 1πu4 1πg*4 | o.e. = 1 | enlace simple |
| Ne2: KK 1σg2 1σu*2 2σg2 1πu4 1πg*4 2σu*2 | o.e. = 0 |
Se define el orbital molecular ocupado de mayor energía, HOMO, como aquel que de acuerdo con el principio de construcción se ocupa en último lugar. Asimismo, el orbital molecular vacío de menor energía, LUMO, es el que sigue en energía al HOMO. A estos dos orbitales moleculares se les conoce como orbitales frontera en las moléculas y juegan un papel muy importante en los estudios cinéticos y estructurales.
Propiedades magnéticas, energía de enlace y distancia de enlace.
Las propiedades magnéticas de algunas de las moléculas descritas en el apartado anterior suponen una verificación de lo propuesto por esta Teoría. La siguiente tabla presenta las características de las mismas en lo que a propiedades magnéticas, energía de enlace y longitud de enlace se refiere.
Resultados de la TOM para moléculas A2.
Molécula |
Electrones |
Enlaces |
Electrones desapareados |
Energía de Enlacea |
Magnetismo (D/P)b |
Longitud de enlacec |
|---|---|---|---|---|---|---|
H2 |
2 |
1 |
0 |
432 |
D |
0.742 |
He2 |
4 |
0 |
0 |
--- |
--- |
--- |
Li2 |
6 |
1 |
0 |
105 |
D |
2.67 |
Be2 |
8 |
0 |
0 |
--- |
--- |
--- |
B2 |
10 |
1 |
2 |
293 |
P |
1.58 |
C2 |
12 |
2 |
0 |
602 |
D |
1.34 |
N2 |
14 |
3 |
0 |
941.7 |
D |
1.09 |
O2 |
16 |
2 |
2 |
493.6 |
P |
1.20 |
F2 |
18 |
1 |
0 |
155 |
D |
141.8 |
Ne2 |
20 |
0 |
0 |
--- |
--- |
--- |
aEn kJ/mol. bD, diamagnética; P, Paramagnética. cEn Å
De la Tabla anterior pueden inferirse algunos comentarios importantes. Por ejemplo, la TOM explica el paramagnetismo de la molécula de O2, como consecuencia de la existencia de electrones desapareados en el orbital 1πg*2. Asimismo, los datos explican igualmente la existencia de los dos tipos de Diagramas que aparecen en la Figura 12. De no ser así, no sería posible explicar el paramagnetismo del B2 o el diamagnetismo del C2 (un esquema general como el de la Figura 12b supondría exactamente lo contrario para estas moléculas: B2 diamagnética y C2 paramagnética).
Es también posible predecir la existencia de especies derivadas de las moléculas de la Tabla anterior por ionización. Tómese, por ejemplo, el caso del oxígeno. Esta molécula puede ionizarse negativa o positivamente:
O2 + 2e ![]() O2=
O2=
O2 - 1e ![]() O2+
O2+
En el primer caso, el del ion peróxido, los dos electrones entran en un orbital molecular antienlazante, lo que disminuye el orden de enlace hasta 1. Ello se traduce en un aumenta de la distancia internuclear, que experimentalmente se ha determinado de 1.49 Å. Por el contrario, la pérdida de un electrón y la consiguiente formación del catión dioxigenilo O2+ supone la disminución en el número de electrones enlazantes, y por ende, una disminución en el orden de enlace hasta 1.5. El resultado es también un elongamiento del enlace O-O hasta 1.26Å.