Cuando dos átomos se aproximan uno a otro hasta que el orbital de uno de ellos comparte una cierta amplitud con el orbital del otro, se dice que ambos orbitales solapan. La magnitud de dicho solapamiento puede ser positiva, negativa o cero, de acuerdo con las propiedades de los orbitales atómicos en cuestión. En la figura se ilustran ejemplos de algunos solapamientos. El signo de este solapamiento entre orbitales da lugar a la formación de orbitales moleculares enlazantes (solapamiento positivo), antienlazante (solapamiento negativo) o de no enlace (solapamiento nulo).
La magnitud del solapamiento es igualmente calculable a partir de la integral del solapamiento S. Extendiendo los conocimientos alcanzados en el estudio del modelo mecano-cuántico del átomo a la molécula, el cuadrado de las funciones de onda moleculares se relaciona con el concepto de probabilidad. Para Ψe y Ψa, sus cuadrados serían:
Ψe2 = φA2 + 2φAφB + φB2
Ψa2 = φA2 - 2φAφB + φB2
La diferencia entre ambas probabilidades es el término 2φAφB. A la integral ∫φAφBdτ se la denomina integral de solapamiento, S, y es de extraordinaria importancia en la Teoría de Orbitales Moleculares. Si S>0, entonces el solapamiento positivo induce un apantallamiento de la repulsión internuclear, y el sistema disminuye su energía hasta la situación enlazante. La situación contraria (S<0) no favorece el enlace pues en realidad los núcleos son empujados uno contra otro, en una situación energética superior a la de partida y, por tanto, de carácter antienlazante.
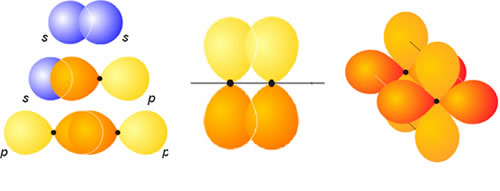
Solapamientos conducentes a orbitales moleculares de tipo sigma (izqda), pi (centro) y delta (derecha).
La representación espacial de un orbital molecular, en lo que a su parte angular se refiere, y al igual que ocurre con los orbitales atómicos, delimita el volumen que encierra la mayor densidad electrónica (>80%). Su forma depende de las funciones de onda moleculares. Del mismo modo que los orbitales atómicos se han clasificado como s, p, d, f, etc. los orbitales moleculares se pueden clasificar de acuerdo con la simetría que muestran respecto de la rotación alrededor del eje del enlace y respecto de la inversión. Así, el orbital molecular enlazante presenta simetría cilíndrica (es simétrico cuando se rota alrededor del eje del enlace que pasa a través de los dos núcleos) y por ello se le denomina orbital σ. Además este orbital es también simétrico respecto de la inversión con respecto al centro de simetría (el signo de la función de onda no cambia), por lo que también recibe el nombre de gerade, g. La nomenclatura completa para dicho orbital molecular es σg.
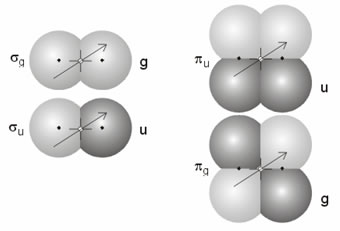
Orbitales moleculares de tipo sigma y de tipo pi.
El orbital molecular de antienlace de la molécula de H2 también es un orbital de tipo σ* (el asterisco representa el carácter antienlazante, o de mayor energía, del orbital molecular), pero es antisimétrico respecto de la inversión, por ello se denomina ungerade, u. Su notación característica completa es la de orbital molecular σu*. Todos los orbitales moleculares antienlazantes poseen un plano nodal perpendicular al eje del enlace. También resulta posible obtener orbitales moleculares de simetría cilíndrica, σ, mediante el solapamiento de otros orbitales atómicos (por ejemplo, a partir de orbitales p).
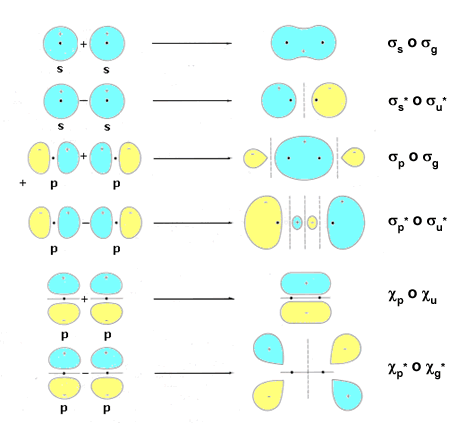
Formas de los Orbitales Moleculares a partir de los orbitales atómicos s y p
El solapamiento lateral de dos orbitales p da lugar a la formación de dos orbitales moleculares, uno de enlace y otro de antienlace, de simetría π. Los orbitales moleculares π presentan un plano nodal que pasa por la zona internuclear. El orbital molecular enlazante π es antisimétrico respecto de la inversión y se representa como πu. El orbital molecular antienlazante π* es simétrico respecto de la inversión y se representa como πg*. La figura muestra un esquema de las formas de los orbitales moleculares generados por los orbitales 1s, 2s y 2p, tanto de tipo σ como de tipo π.