La Teoría de Orbitales Moleculares (T.O.M.) es la segunda aproximación al estudio del enlace covalente, y la más ampliamente empleada para explicar la estructura y la geometría de muchos sólidos inorgánicos. El punto de partida consiste en asumir que si los dos núcleos implicados en el enlace se ubican a la distancia de equilibrio, los electrones se alojarán no en orbitales atómicos de cada elemento, sino en orbitales moleculares, que son análogos a los atómicos, y que presentan características similares, como se verá más adelante. Esta analogía es de tal grado que al igual que ocurría con los átomos polielectrónicos, no es posible resolver la ecuación de Schrödinger de forma exacta para la molécula, y de nuevo hay que recurrir a métodos aproximados para conocer la forma de las funciones de onda que representen los mencionados orbitales moleculares.
Uno de los métodos más empleados es el que hace uso de las Combinaciones Lineales de Orbitales Atómicos (CLOA). Esta aproximación puede entenderse de forma simple si se piensa que cuando un electrón esté cerca de uno de los núcleos, es decir, cuando esté “controlado” por un núcleo, su función de onda será muy similar a la de un orbital atómico. Los orbitales moleculares de la molécula de H2 se obtienen de forma aproximada mediante la combinación lineal de los orbitales atómicos 1s de cada átomo de hidrógeno. Únicamente se pueden escribir dos combinaciones lineales:
Ψ+ = cAφA +cBφB
Ψ- = cAφA – cBφB
Los coeficientes ci que aparecen en la combinación lineal reflejan la contribución de cada orbital atómico al orbital molecular: cuanto mayor sea el valor del coeficiente mayor será la participación del orbital atómico en el molecular. Para la molécula de H2 la contribución de ambos orbitales atómicos a los orbitales moleculares es la misma, esto es, cA = cB = 1, de forma que las expresiones matemáticas de las funciones de onda se pueden simplificar:
Ψ+ = φA + φB
Ψ- = φA – φB
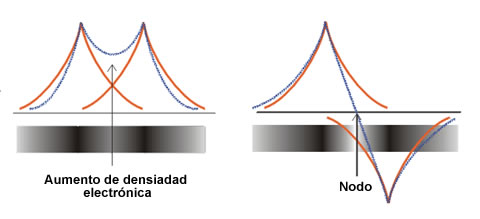
Ψ + (izquierda) y Ψ- (derecha)
En la figura anterior se representan las funciones Ψ+ y Ψ- (parte radial) frente a la distancia internuclear. La función Ψ+ concentra la densidad electrónica entre los dos núcleos, debido a una interferencia constructiva φA y φB, lo que aumenta la amplitud en la región internuclear. Por el contrario, la función de onda Ψ- concentra la densidad electrónica fuera de la zona comprendida entre los dos núcleos. La interferencia de tipo destructivo entre las funciones de onda φA y φB cancela sus amplitudes y da lugar a la formación de un plano nodal en la región internuclear. Obviamente, la molécula será más estable si los electrones se encuentran en el orbital Ψ+, porque esto origina un aumento de la atracción electrón-núcleo y una disminución de las repulsiones nucleares. La combinación Ψ+ = φA + φB corresponde al orbital molecular de menor energía y se denomina orbital molecular enlazante, que ahora se representa como Ψe. Por el contrario, la combinación Ψ- = φA – φB, representa al orbital molecular de mayor energía denominado orbital molecular antienlazante (Ψa). Las energías relativas de los dos orbitales moleculares se muestran en la siguiente figura, que constituye un ejemplo de lo que se conoce como Diagrama de Orbitales Moleculares o Diagrama de Niveles de Energía.
De forma análoga a las limitaciones en el caso de átomos, el principio de exclusión de Pauli limita a dos el número de electrones que pueden ocupar un orbital molecular, lo que obliga a su apareamiento. La molécula de H2 posee una energía menor que los dos átomos de H por separados porque los dos electrones ocupan el orbital molecular enlazante y ambos contribuyen a una disminución de la energía del sistema.
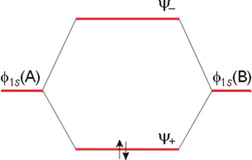
Diagrama de Orbitales Moleculares de la molécula de Hidrógeno.
En definitiva, el enlace en la molécula de hidrógeno puede ahora explicarse en función de la formación de dos orbitales moleculares a partir de dos orbitales atómicos. De forma general, N orbitales atómicos pueden conducir a la formación de N orbitales moleculares. Los electrones ocuparán los Orbitales moleculares siguiendo las mismas reglas que las especificadas para las configuraciones electrónicas de los elementos.